Algorithms
Last Updated :
15 Feb, 2023
Learn more about Algorithms in DSA Self Paced Course
Practice Problems on all Algorithms
Recent articles on Algorithms
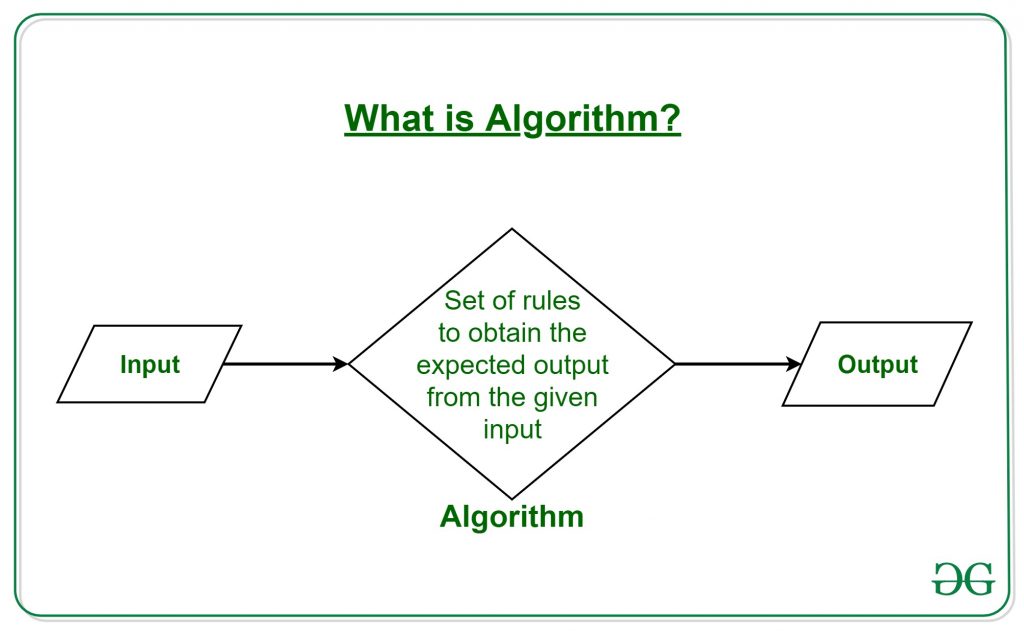
What is an Algorithm?
The word Algorithm means ” A set of rules to be followed in calculations or other problem-solving operations ” Or ” A procedure for solving a mathematical problem in a finite number of steps that frequently by recursive operations “.
Therefore Algorithm refers to a sequence of finite steps to solve a particular problem.
Algorithms can be simple and complex depending on what you want to achieve.
Types of Algorithms:
There are several types of algorithms available. Some important algorithms are:
1. Brute Force Algorithm: It is the simplest approach for a problem. A brute force algorithm is the first approach that comes to finding when we see a problem.
2. Recursive Algorithm: A recursive algorithm is based on recursion. In this case, a problem is broken into several sub-parts and called the same function again and again.
3. Backtracking Algorithm: The backtracking algorithm basically builds the solution by searching among all possible solutions. Using this algorithm, we keep on building the solution following criteria. Whenever a solution fails we trace back to the failure point and build on the next solution and continue this process till we find the solution or all possible solutions are looked after.
4. Searching Algorithm: Searching algorithms are the ones that are used for searching elements or groups of elements from a particular data structure. They can be of different types based on their approach or the data structure in which the element should be found.
5. Sorting Algorithm: Sorting is arranging a group of data in a particular manner according to the requirement. The algorithms which help in performing this function are called sorting algorithms. Generally sorting algorithms are used to sort groups of data in an increasing or decreasing manner.
6. Hashing Algorithm: Hashing algorithms work similarly to the searching algorithm. But they contain an index with a key ID. In hashing, a key is assigned to specific data.
7. Divide and Conquer Algorithm: This algorithm breaks a problem into sub-problems, solves a single sub-problem and merges the solutions together to get the final solution. It consists of the following three steps:
8. Greedy Algorithm: In this type of algorithm the solution is built part by part. The solution of the next part is built based on the immediate benefit of the next part. The one solution giving the most benefit will be chosen as the solution for the next part.
9. Dynamic Programming Algorithm: This algorithm uses the concept of using the already found solution to avoid repetitive calculation of the same part of the problem. It divides the problem into smaller overlapping subproblems and solves them.
10. Randomized Algorithm: In the randomized algorithm we use a random number so it gives immediate benefit. The random number helps in deciding the expected outcome.
Topics:
Analysis of Algorithms:
- Asymptotic Analysis
- Worst, Average and Best Cases
- Asymptotic Notations
- Lower and Upper Bound Theory
- Introduction to Amortized Analysis
- What does ‘Space Complexity’ mean?
- Polynomial Time Approximation Scheme
- Accounting Method | Amortized Analysis
- Potential Method in Amortized Analysis
Searching and Sorting:
- Introduction to Searching Algorithms
- Introduction to Sorting Algorithm
- Stable and Unstable Sorting Algorithms
- Lower bound for comparison based sorting algorithms
- Can Run Time Complexity of a comparison-based sorting algorithm be less than N logN?
- Which sorting algorithm makes minimum number of memory writes?
Greedy Algorithms:
- Introduction to Greedy Algorithms
- Activity Selection Problem
- Huffman Coding
- Job Sequencing Problem
- Quiz on Greedy Algorithms
- Minimum Number of Platforms Required for a Railway/Bus Station
Dynamic Programming:
- Introduction to Dynamic Programming
- Overlapping Subproblems Property
- Optimal Substructure Property
- Longest Increasing Subsequence
- Longest Common Subsequence
- Min Cost Path
- Coin Change
- Matrix Chain Multiplication
- 0-1 Knapsack Problem
- Longest Palindromic Subsequence
- Palindrome Partitioning
Pattern Searching:
- Introduction to Pattern Searching
- Naive Pattern Searching
- KMP Algorithm
- Rabin-Karp Algorithm
- Pattern Searching using a Trie of all Suffixes
- Aho-Corasick Algorithm for Pattern Searching
- Z algorithm (Linear time pattern searching Algorithm)
Backtracking:
- Introduction to Backtracking
- Print all permutations of a given string
- The Knight’s tour problem
- Rat in a Maze
- N Queen Problem
- Subset Sum
- m Coloring Problem
- Hamiltonian Cycle
- Sudoku
Divide and Conquer:
- Introduction to Divide and Conquer
- Merge Sort
- Write your own pow(x, n) to calculate x*n
- Count Inversions
- Closest Pair of Points
- Strassen’s Matrix Multiplication
Geometric Algorithm:
- Introduction to Geometric Algorithms
- Closest Pair of Points | O(nlogn) Implementation
- How to check if a given point lies inside or outside a polygon?
- How to check if two given line segments intersect?
- Given n line segments, find if any two segments intersect
- How to check if given four points form a square
- Convex Hull using Jarvis’ Algorithm or Wrapping
Mathematical Algorithms:
- Introduction to Mathematical Algorithms
- Write an Efficient Method to Check if a Number is Multiple of 3
- Write a program to add two numbers in base 14
- Program for Fibonacci numbers
- Average of a stream of numbers
- Multiply two integers without using multiplication, division and bitwise operators, and no loops
- Babylonian method for square root
- Sieve of Eratosthenes
- Pascal’s Triangle
- Given a number, find the next smallest palindrome
- Program to add two polynomials
- Multiply two polynomials
- Count trailing zeroes in factorial of a number
Bitwise Algorithms:
- Introduction to Bitwise Algorithms
- Little and Big Endian
- Detect opposite signs
- Swap bits
- Turn off the rightmost set bit
- Rotate bits
- Next higher number with same number of set bits
- Swap two nibbles in a byte
Graph Algorithms:
- Introduction to Graph Algorithms
- BFS, DFS
- Cycles in Graph
- Shortest paths
- MST
- Topological Sorting
- Connectivity
- Max Flow
Randomized Algorithms:
- Introduction to Randomized Algorithms
- Linearity of Expectation
- Expected Number of Trials until Success
- Randomized Algorithms | Set 0 (Mathematical Background)
- Randomized Algorithms | Set 1 (Introduction and Analysis)
- Randomized Algorithms | Set 2 (Classification and Applications)
- Randomized Algorithms | Set 3 (1/2 Approximate Median)
- Reservoir Sampling
Branch and Bound:
- Branch and Bound | Set 1 (Introduction with 0/1 Knapsack)
- Branch and Bound | Set 2 (Implementation of 0/1 Knapsack)
- Branch and Bound | Set 3 (8 puzzle Problem)
- Branch And Bound | Set 4 (Job Assignment Problem)
- Branch and Bound | Set 5 (N Queen Problem)
- Branch And Bound | Set 6 (Traveling Salesman Problem)
Quizzes:
Please see Data Structures and Advanced Data Structures for Graph, Binary Tree, BST and Linked List based algorithms.
Share your thoughts in the comments
Please Login to comment...